2022-09-18 mon （祝）


「　『連単位データベース』がどういう構造か　考えるか……」


「　結局やるのか」


「　それはデータベースなの？」


「　まず、『連単位』について説明しよう」




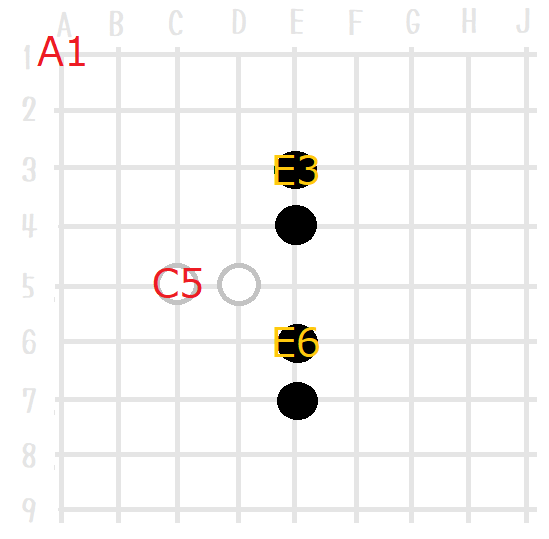
「　↑　『連単位』という考え方では、　盤上の最小単位は　『連』　だぜ。
石は　存在しなくなるぜ」


「　石が存在しない盤の絵を　描いてくれだぜ」




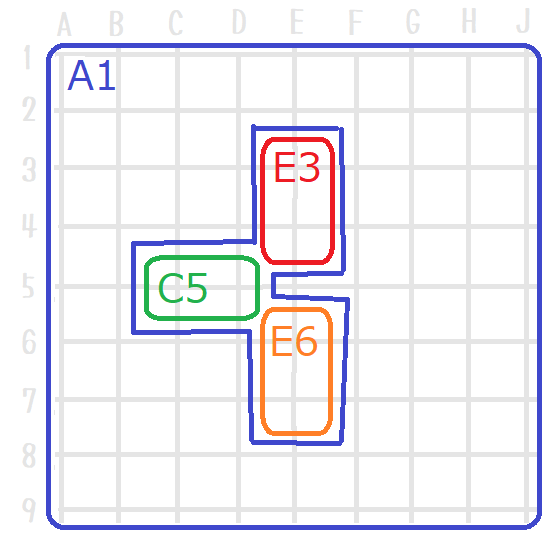
「　↑　こうかな」


「　こんな　角切り餅が　何の役に立つの？」




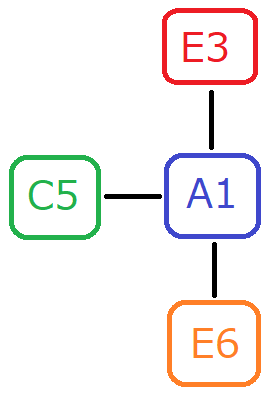
「　↑　隣接する連はどれか、という関心事が中心になるということだぜ」


「　囲碁盤の上で　石を１個置くだけで　『連単位』のグラフが
どれほど　変容するか　明らかにしてくれだぜ」




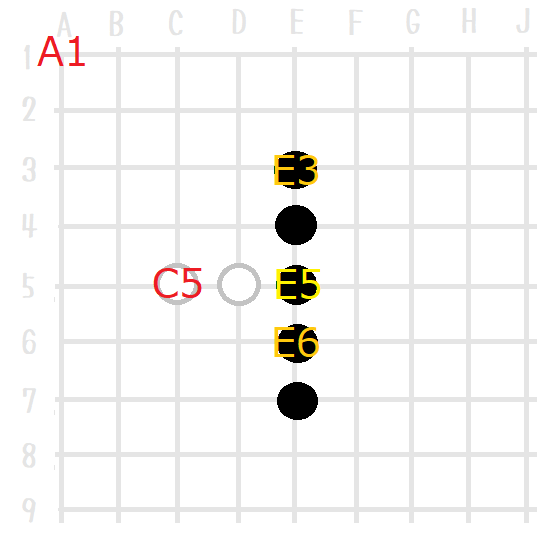
「　↑　じゃあ　まずは　『石単位』　で　Ｅ５　に石を置いてみようぜ？」




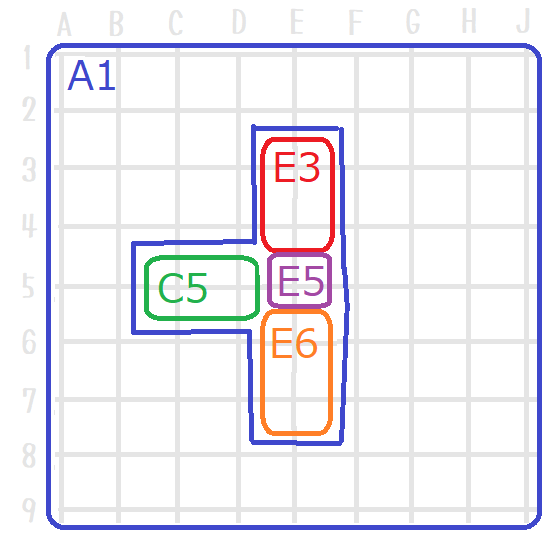
「　↑　『連単位』　で見ると　こうだな」


「　『石単位』を廃止して　『連単位』だけに　できないの？」


「　できないぜ」


「　なんでだぜ？」


「　初期局面や、途中局面からの再開のときに　『石単位』の盤　で送信されてくるのと、
人間は囲碁を　『石単位』の盤　で見たいからだぜ」


「　ぷよ碁　は『連単位』の見た目をしてますけどね」




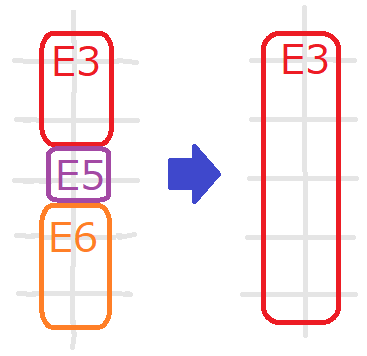
「　↑　ここで、　くっつく　とは、足し算ではなく　引き算であることに
注意してほしい」


「　面白い空間だぜ」




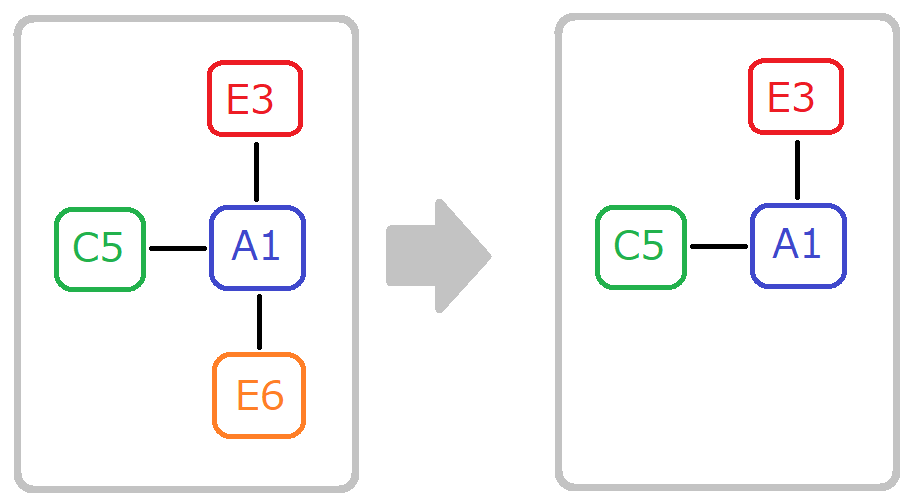
「　↑　『連単位』グラフで　右図を見ると、
Ｅ５　を足したのではなく、　Ｅ６を切った　という操作にしか見えないな」


「　囲碁をやっているようには　見えないな」


「　このような変化を全パターン見せなさいよ」


「　わらう」




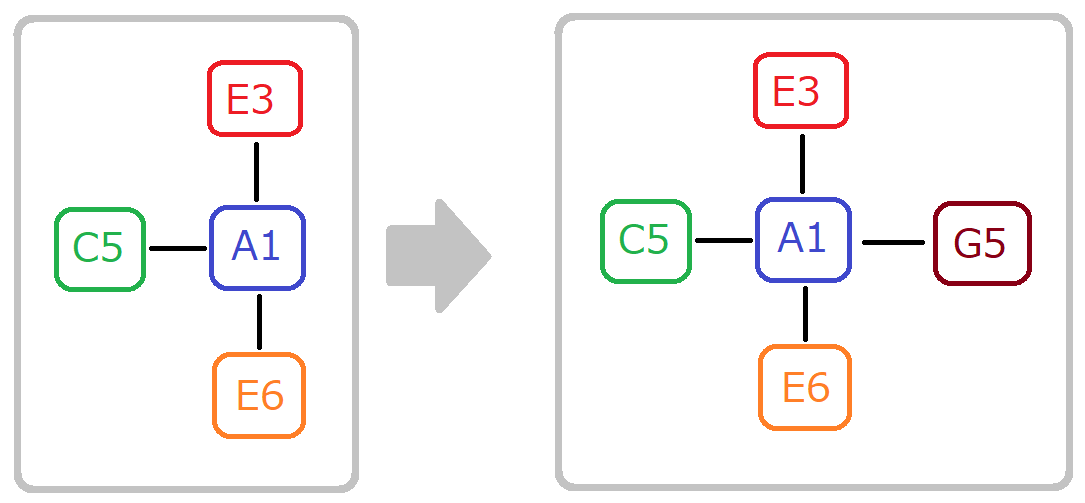
「　↑　図を描くのが　めんどくさいから　G5　を感じてくれだぜ」


「　すぐ横着するの　わらう」




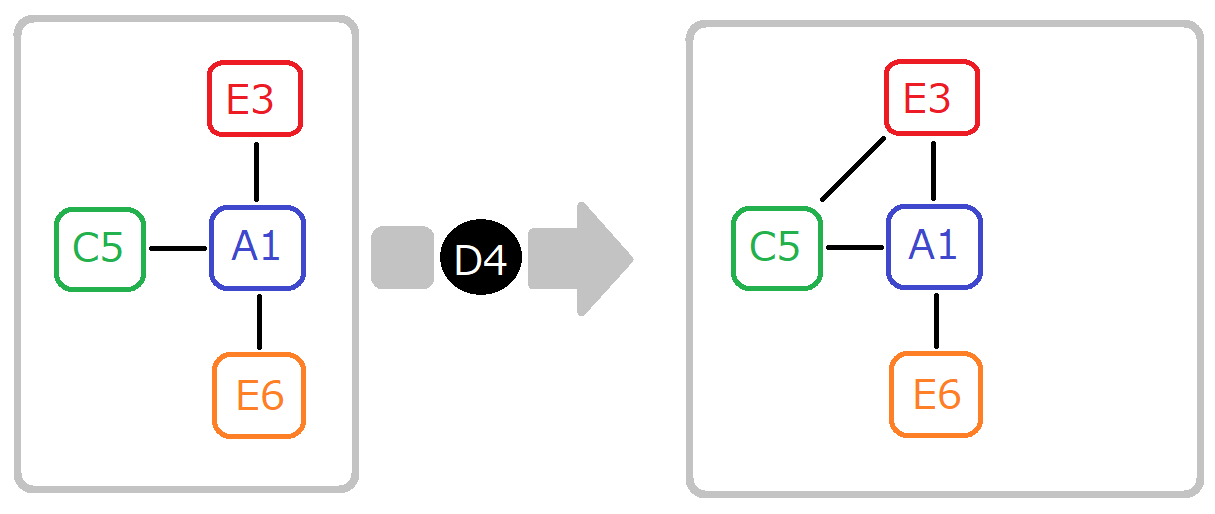
「　↑　ただ　接続が増えるだけ、　というケースもあるぜ」


「　石を打ち上げることを考えなければ、
新規のノードは　最大で１つ増えるかで、
既存のノードは　０～４つ減るかで、
エッジは　０～４つ増えることがあるのよ
エッジが減るのは　ノードが消えるときに巻き込まれて消えるだけで、
その数は　ぱっと　は分からないわねぇ」


「　大盤で解説してくれだぜ」




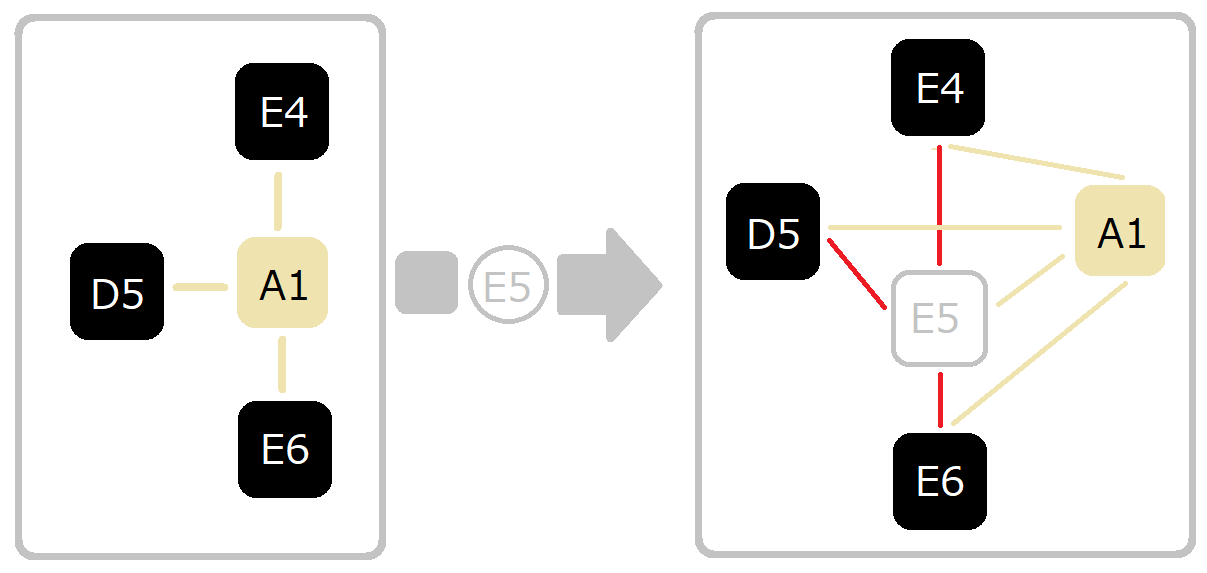
「　↑　石の打ち上げを考えないときで　エッジが増える最大のケースは、
異なる色の石３つと、空点と隣接する　新しい石が増えたときだぜ」


「　石の打ち上げがないのに　異なる色の石４つと隣接するのは　着手禁止点だしな」


「　盤端（ばんたん）に石を置くと　エッジの最大数は　１～２本　減るわね」




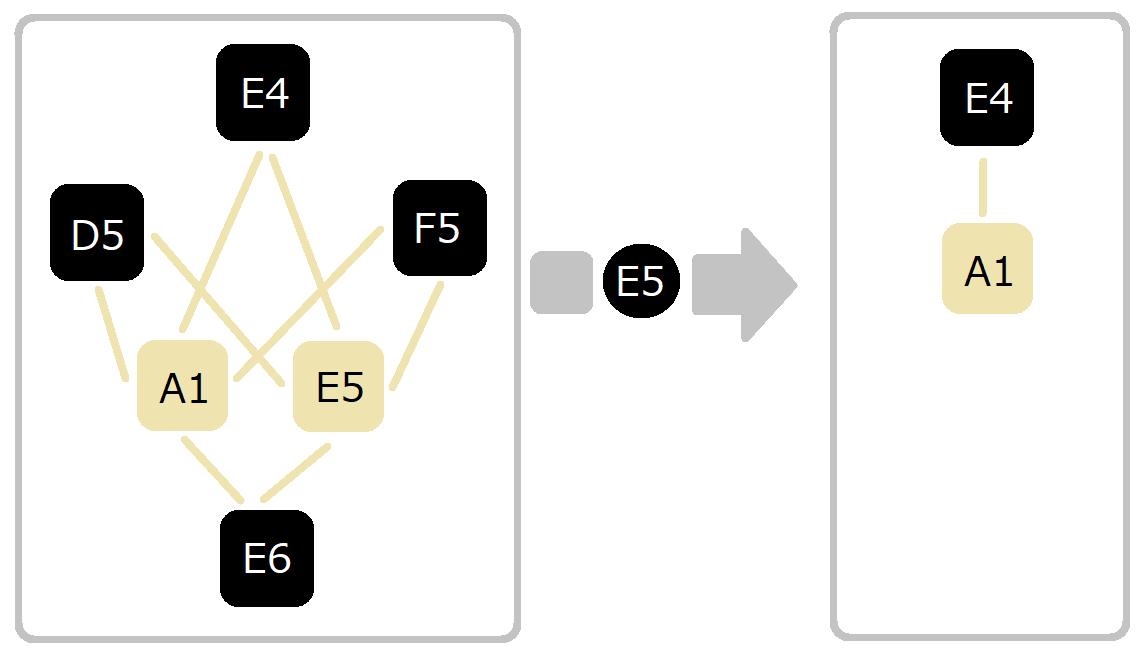
「　↑　自分の眼を潰すと　エッジが最大で７本消えるぜ」


「　ドラゴンの紋章みたいだな」


「　内海を囲っているのと、外海を囲っているのと　どちらの見方もできるケースがあるから
二重構造のようなケースが出てきて　二重網　みたいになるのよ」




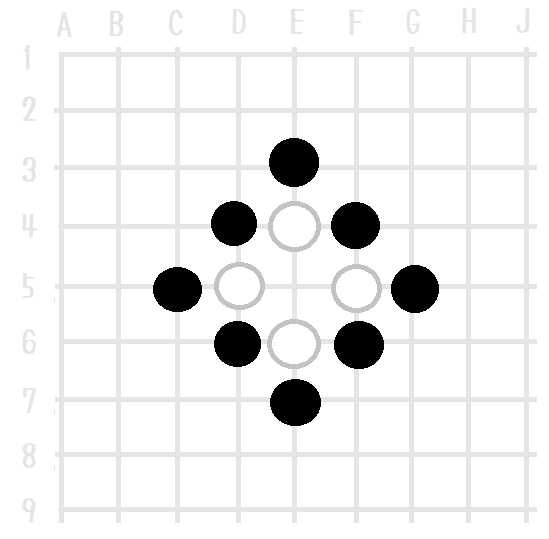
「　↑　石を打ち上げるケースも　考えてみるかだぜ」




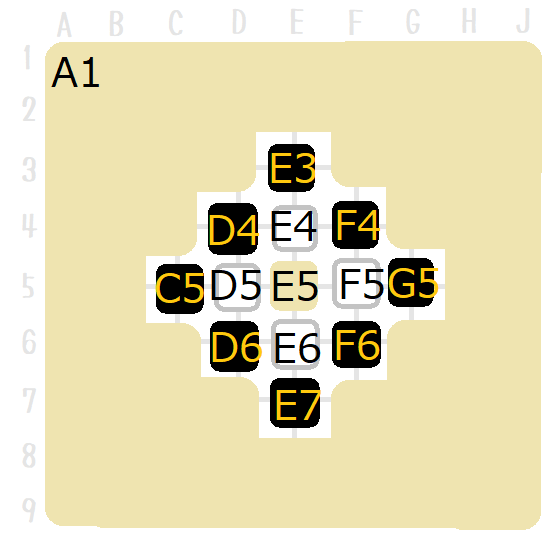
「　↑　連単位にすると　こうだな」




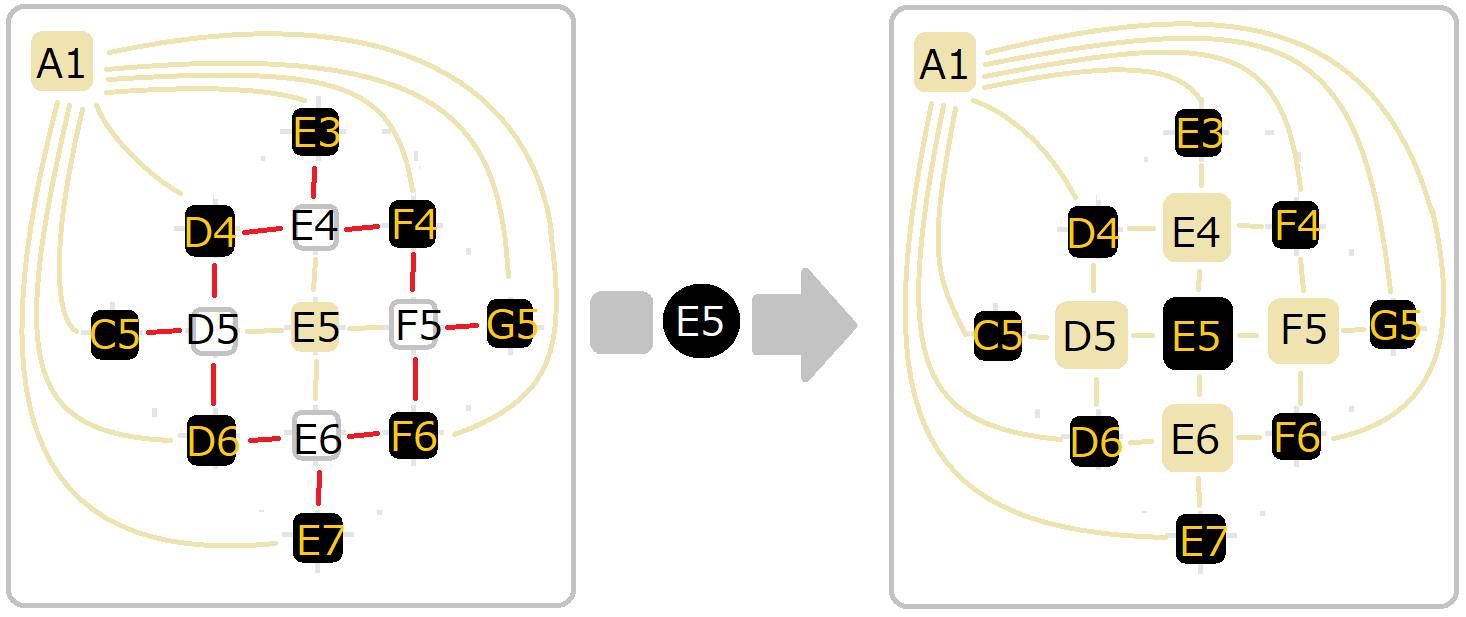
「　↑　ノード５つの色が変わっただけだぜ。
エッジは　増えてもないし、減ってもないぜ」


「　希望が見えてきたな」


「　確かに　石を打ち上げるときは　反対側の石に敷き詰められているし、
石と空点が　入れ替わっているだけで　連の形は　変わんないわね」


「　今日は遅くなったので　ここまでとするぜ」

2022-09-19 tue